Geometria Plana - Introdução e ângulos

CONCEITOS BÁSICOS INICIAIS

O estudo dos ângulos é fundamental para compreender conceitos ligados a geometria, trigonometria, entre outros ramos da Matemática. O estudo dos ângulos é um dos responsáveis pelos avanços que possuímos atualmente em vários ramos, como a navegação e a astronomia. Um exemplo notável é o astrolábio náutico (inventado pelo grego Hiparco) usado para medir ângulos. Nos séculos V e VI, os navegadores construíram esse instrumento para medir a elevação das estrelas e do sol com o intuito de localizar suas embarcações. Mais tarde, o astrolábio deu origem ao sextante, mais simplificado, mas que cumpria a mesma função.

ÂNGULOS 

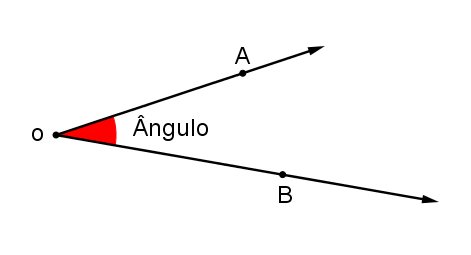
Chama-se ângulo a região entre duas semirretas que partem de uma mesma origem. Podemos dizer, ainda que um ângulo é a medida da abertura de duas semirretas que partem da mesma origem.

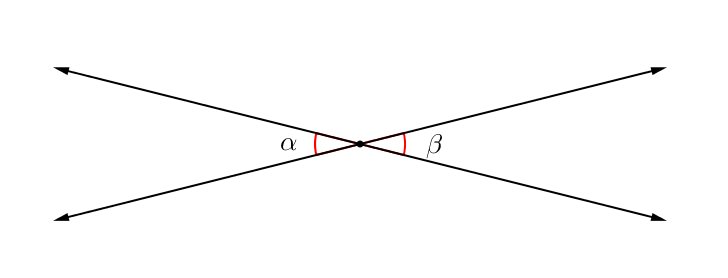
Ângulos opostos pelo vértice

Dizemos que dois ângulos são opostos pelo vértice se as semirretas que os formam partem do mesmo vértice e são opostas aos lados do outro.

Bissetriz

A bissetriz de um ângulo é a semirreta que parte do vértice do ângulo e o divide em dois ângulos congruentes (iguais).

Classificação

Ângulo raso: ângulo com medida igual a 0º ou 180º.

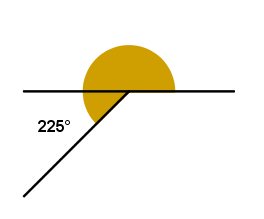
Ângulo Côncavo: ângulo com medida entre 180º e 360º.

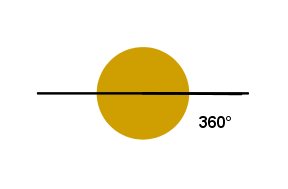
Ângulo completo ou de uma volta: ângulo com medida igual a 360°.

Ângulos complementares

Dois ângulos são complementares se a soma de suas medidas for 90º um deles é o complemento do outro

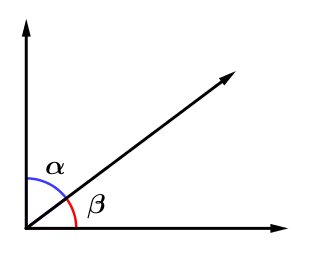
α+β=90

Ângulos suplementares

Dois ângulos são suplementares se a soma de suas medidas for 180º um deles é o suplemento do outro

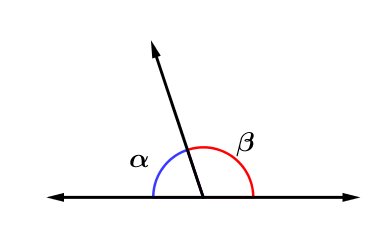
α+β=180o

Ângulos replementares

Dois ângulos são replementares quando a sua soma for igual a 360°.

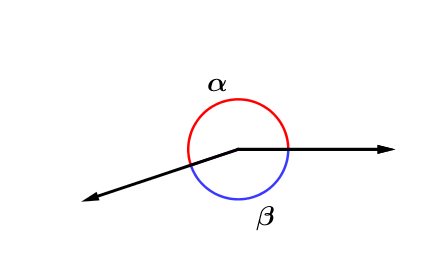
α+β=360o

Unidades de medida de um ângulo

Grau (°)

A unidade principal de medida de um ângulo é o grau (°).

1° (um grau) equivale a 1360 de uma circunferência, ou seja, 1° corresponde a uma das 360 partes em que uma circunferência foi dividida. Assim, uma circunferência inteira possui 360°.

Minuto ( ‘ )

Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida minuto ( ‘ ). Um minuto corresponde a 160 de um grau, ou seja, 1 minuto (1’) corresponde a uma das 60 partes em que um ângulo de 1° foi dividido.

1′=1o60

Um grau possui 60 minutos (1º = 60').

Segundo ( '' )

Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida segundo ( '' ). Um segundo corresponde a 160 de um minuto, ou seja, 1 segundo (1'') corresponde a uma das 60 partes em que um ângulo de 1' foi dividido.

1′′=1′60

Um minuto possui 60 segundos (1' = 60'').

Grado

Esta medida não é muito usual.

Um grado corresponde a 910 de um grau, ou seja, 1 grado (1 gr) corresponde a 9 das 10 partes em que um ângulo de 1° foi dividido.

Retas paralelas cortadas por uma transversal 

Ângulos correspondentes: a e e, d e h, b e f, c e g                  Congruentes

Ângulos colaterais externos: a e h, b e g                                Suplementares

Ângulos colaterais internos: e e d, c e f                                  Suplementares

Ângulos alternos externos: a e g, b e h                                   Congruentes

Ângulos alternos internos: d e f, c e e                                     Congruentes

clique aqui para mais conteudo

SLIDES PARA APOIO


Você conseguirá aprender melhor matemática com auxilio de várias vídeo aulas, a teoria escrita complica um pouco!